定时同步算法

频域匹配滤波联合O&M算法定时同步

根据林长星的论文，可以在频域匹配滤波的时候使用延迟系数进行补偿，以达到定时同步的目标。其实现框图如下图所示。首先下变频后的数据会进行FFT运算，在频域对匹配滤波器系数进行FFT后的数值进行点乘，模拟时域的卷积运算，卷积完后的数据会与NCO算出来的定时误差进行频域的系数相乘操作，以实现时域数据的偏移，之后做IFFT得到最终匹配滤波与定时同步后的数据。定时同步后的数据会送入定时误差估计模块中，利用O&M算法进行定时误差的无偏估计，得到误差估计值$\hat{\varepsilon}$，该误差估计值$\hat{\varepsilon}$会被送入环路滤波器进行环路滤波，NCO则会对环路滤波的输出数据$\varepsilon$进行溢出控制。

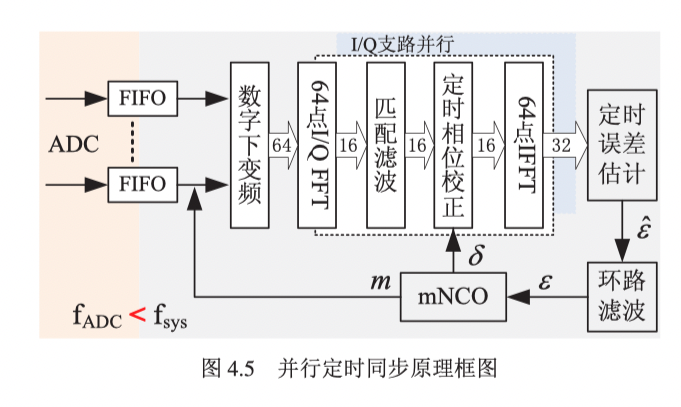
O&M定时误差估计算法

O&M算法是由Oerder和Meyr由1988年提出的，这种算法需要至少4倍过采样，但是其误差估计值是真实值的无偏估计，在高信噪比下渐进等价于最大似然估计，而且算法对信噪比和载波频偏都不敏感，性能上会比Gardner算法更好，其主要推导过程如下。

假设接收到的通过信道后的信号为

$$ \begin{equation} \begin{aligned} r(t) &=\sum_ {n=-\infty}^{\infty} a_ {n} g_ {T}(t-n T-\varepsilon(t) T)+n(t) \ &=u(t)+n(t) . \end{aligned} \end{equation} $$

其中，$a_ n$ 为复信号（若为QPSK，则取值为 $\pm 1, \pm i$ ，即4个点在坐标轴上），$g_T(t)$为传输信号的单位脉冲响应，$T$是符号持续时间，$n(t)$为信道噪声，这里假设为功率密度是$N_0$的高斯白噪声，定时误差$\varepsilon(t)$未知，且随时间变化缓慢。

由于定时误差$\varepsilon$变化很慢，在数字实现的时候，可以将信号分片，对于每一片信号$\Delta_m$，我们可以假设$\varepsilon$是一个常数，其估计值为$\hat{\varepsilon}$。该定时误差估计值需要与之前时刻的估计值进行结合（即需要进行滤波）以获得最佳估计值$\bar{\varepsilon}$，这个最佳估计值用于控制检测的采样器。

假设接收端的冲激响应为$g_R(t)$，则接收到的信号为$\tilde{r}(t)=r(t) * g_{R}(t)$，设采样率为$N/T$，则接收端采样值为$\tilde{r}_ {k}=\tilde{r}(k T / N)$，则接收端序列取平方后有

$$ \begin{equation} x_{k}=\left|\sum_{n=-\infty}^{\infty} a_{n} g\left(\frac{k T}{N}-n T-\varepsilon T\right)+\tilde{n}\left(\frac{k T}{N}\right)\right|^{2} \end{equation} $$

其中$g(t)=g_ {T}(t) * g_{R}(t)$。上式代表对接收信号进行滤波以及平方之后的采样值，其频谱在$1/T$处有一个分量。

对上述取平方后的序列以时长$LT$进行分片（即每个分片有$LN$个符号），对序列以符号速率求复傅里叶级数

$$ X_{m}=\sum_{k=m L N}^{(m+1) L N-1} x_{k} e^{-j 2 \pi k / N} $$

上述级数求归一化相位可得$\hat{\varepsilon}_ m=-1 / 2 \pi \arg \left(X_{m}\right)$，可以得出该归一化相位$\hat{\varepsilon}_m$是定时误差$\varepsilon$的无偏估计。证明请直接参考原文章。

这里值得注意的是，$\arg()$算符并不等价于$\arctan()$算符，因为$\arctan()$的值域是$\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$，但$\arg()$算符求的是当前的复向量的角相位，对应的值域是$\left(-\pi, \pi\right)$。

思考：为何上式频谱会在$1/T$处有的分量？

可以参考书籍《Digital Signal Processing Fundamentals and Applications》Fig. 4.3对于一个符号周期为$T$的信号，其频率为$f_0$，若以采样率$f_s=Nf_0=N/T$进行采样，则其频谱应该会在0-$fs$（即0-$Nf_0$）处有N个间隔为$f_0$的值，即上式一定会在$1/T$处有分量。这也证明了为何O&M算法需要大于2倍过采样，因为如果只有两倍过采样的话，在0-$f_s$频率范围内，只有N+1根谱线，分别为0, 1/T, 2/T这几根谱线，并且不满足奈奎斯特采样率，因此在1/T处会产生混叠，造成采集的数据不准确，影响后续的判断。

O&M算法的特点

O&M算法的特点如下：

• 至少需要4倍过采样
• 估算出来的定时误差$\hat{\varepsilon}$是真实定时误差的无偏估计
• 可以用于前馈也可以用于反馈结构
• 对频偏不敏感
• 对信噪比不敏感
• 前馈结构适用于突发通信

Gardner算法

阅读论文《A BPSK/QPSK Timing-Error Detector for Sampled Receivers》

Gardner算法基本公式

$$ \begin{aligned} u_{t}(r)=y_{I}(r-\frac{1}{2})[&\left.y_{I}(r)-y_{I}(r-1)\right] \\ &+y_{Q}(r-\frac{1}{2})\left[y_{Q}(r)-y_{Q}(r-1)\right] \end{aligned} $$

其中，$y_I(r)$中的$r$ 代表符号索引，It is convenient to denote the strobe values of the $r$th symbol- as $y_I(r)$ and $y_Q(r)$. 这里的strobe不太确定到底指的是采样值还是内插后的值。那么，在两个strobe之间的那个点的值就是$y_{I}(r-\frac{1}{2})$和 $y_{Q}(r-\frac{1}{2})$。这就是利用采样点计算出来定时误差$u_t(r)$的Gardner误差估计公式。

Gardner算法的特点

优点：

• 只需要两倍过采样

缺点：

• 需要40%-100%的额外带宽

为什么需要40%-100%的额外带宽呢？

因为如果带宽过窄会引入自噪声。

为什么会引入自噪声？自噪声哪里来的？

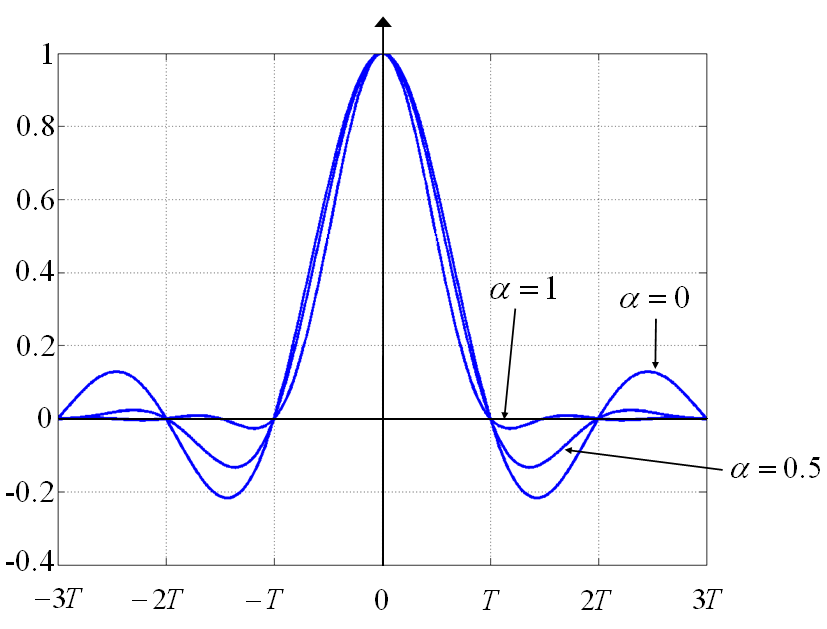
看上图，如果$\alpha=1$的话，即频谱扩展100%，可以看见1.5T处为0，这个时候采样$y_{I}(r-\frac{1}{2})$和 $y_{Q}(r-\frac{1}{2})$时不是处于过零点处，在计算定时误差时就会呈现散点的形式（而非零点），这种情况在求均值后是没问题的，关键就是如果只看局部，就会引入自噪声，而且随着$\alpha$的减小，自噪声也越大。

Gardner定时误差公式解释

这条公式看上去很简单，也有很多不同的解释，但直接对这条公式进行的解释都是浮于表面的，也无法得知公式到底是怎么被想出来的，不如我们直接对Gardner的原文重新推导一遍，尝试得到原汁原味的思路。这里先给出Gardner原文对公式的解释。

A physical explanation can be ascribed. The detector samples the data stream midway between strobe locations in each of the $I$ and $Q$ channels. If there is a transition between symbols, the average midway value should be zero, in the absence of timing error. A timing error gives a nonzero sample whose magnitude depends upon the amount of error, but either slope is equally likely at the midway point so there is no direction information in the sample alone.

To sort out these different possibilities, the algorithm examines the two strobe values to either side of the midway sample. If there is no transition, the strobe values are the same, their difference is zero, and so the midway sample is rejected. (No timing information is available in the absence of a transition.)

If a transition is present, the strobe values will be different; the difference between them will provide slope information. The product of the slope information and the midway sample provides timing-error information.

按照我的理解尝试一下翻译过来，避免遗忘。检测器会对数据流的 $I$ 路和 $Q$ 的符号采样值(strobe)间的中间点(midway)进行采样（即式中的$y(r-1/2)$）（这个strobe的意思大意就是符号的最佳采样点处，但其实对于这篇论文，当时Gardner还没有提出定时同步环路，仅针对定时误差检测而言，此处的strobe不能直接理解为最佳采样点，而是一个正常的采样点，即该符号对应的其中一个采样点，为一个strobe，隔壁符号的对应的采样点，则为另一个strobe。举个例子，如果当前过采样倍数为4，若假设当前符号的第二个采样点为strobe，即 $y(r-1)$ ，则隔壁的strobe则在当前采样点往后顺延4个，即为下一个strobe， $y(r)$ 。midway的意思其实就是对于接收到的电平信号两个strobe之间的中点，还是以过采样倍数为4为例，如果当前采样序列的索引为1/2/3/4/5/6/7/8，若2为第一个strobe， $y(r-1)$ ，则4为midway， $y(r-1/2)$ ，6为第二个strobe， $y(r)$。而对于加了反馈环路的Gardner环来说，这里的strobe其实就是内插出来的最佳采样点了，不然每次都是用采回来的点进行求解，定时误差永远都不会收敛）。如果两个符号间有跳变，则在没有定时误差的情况下，midway点的平均值应该为0。定时误差会导致midway点采样值不为0，而该值的幅度会取决于误差的大小，不过如果公式中只有中间点这一项的话，还没办法得到位置信息，即超前还是滞后。

为了得到位置信息，算法对midway两端的符号采样值进行衡量，即式中的$y(r)-y(r-1)$，如果两个符号间没有跳变，则两个符号采样值应该是相同的，即差值为0，那么中间相就被消掉了，此时没有定时信息（即如果没有跳变的话，是无法获取定时误差信息的）。

如果有跳变，则符号采样值会不一样，该差值会提供斜率信息。斜率信息与midway值相乘会提供定时误差信息。

Gardner定时误差公式的推导

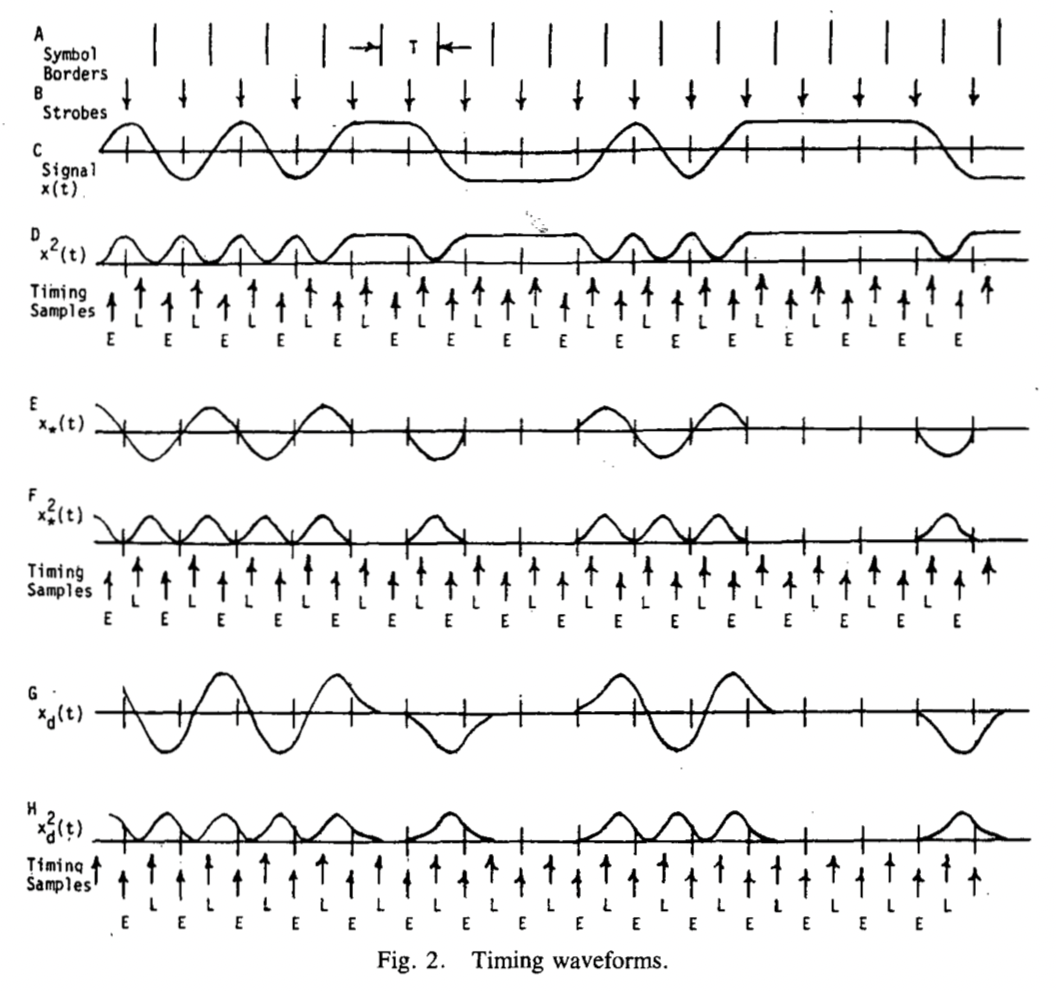
先看图，

• 线A给出了符号的边界，符号的持续时间为$T$。
• 线B给出了最佳采样点的位置，即每个符号间隔的中间点处。
• 线C给出了一个基带信号，该基带信号经过了成型以及匹配，并且满足奈奎斯特准则，是个带限信号，且成型系数用的100%。

如何通过数据流重建一个时钟波形呢？一个已经被证明过的方法是将信号通过一个简单的整流器，如果采用平方律整流器的话，其实就是将数据进行平方。如线D所示，平方完后的信号有如下好处：

• 噪声性能将近最优，尤其是在低信噪比时；
• 如果一个纯sin信号输入，则输出为一个二倍频的sin信号；
• 平方运算是该方法中唯一的非线性操作，该非线性操作在数学上是易于处理的；
• 该平方律整流器在I路和Q路将能独立恢复出载波相位的时钟波形，这在捕获阶段是比较重要的。

利用线D，可以将原型时钟(protoclock)生成出来，具体做法是，利用一个以符号速率为周期的纯sin波形，在数据非跳转处进行隔开，只在数据跳转处进行保留。这个原型时钟再通过一个窄带滤波器或者一个锁相环即可将想要的时钟线恢复出来，并且能消掉各种其他干扰，这就是模拟时钟恢复的方法。

仔细分析可以发现，这个方法其实也可以用于数字系统中，但是并不方便，一个是运算量较大，另一个是仅两个采样点还不太够用，因为sin的周期等于符号周期，而sin一个周期仅两个采样点是不满足采样定律的，所以在数字系统，这个做法需要改进才能用。不过我们不是要重建原型时钟，而是要找到一个方法来计算定时误差，本质上是不需要重建原型时钟的。

线E和线F对应一种预滤波方法(prefilter method)，由于Gardner没用这个方法，此处不再赘述。这是为了改进线D用到的方法而被提出的，有文献可以参考。

延迟差分方法（Gardner用的方法）。

令差分器能进行如下运算：

$$ x_{d}(t)=x(t)-x\left(t-t_{d}\right) $$

其中 $t_d$ 是一个预先算好的延迟时间。值得一提的是，假设 $t_d=T/2$ 则$x_d$的平均延时为$T/4$，即采样时刻与计算出来的定时误差时刻的时间偏移值（这里我理解还不够透彻，为什么平均延时为$T/4$，不过无伤大雅）（我的理解是，线D和线E算出来在时间上是与原信号对齐的，而用这个公式算出来会差$T/4$）。

令 $t_d=T/2$ ，则线C进行延迟差分后可以得到线G。线G跟线E类似，不过线G并不是一个特定的信号波形（线E是一个sin信号）。这个线G有着跟线E几乎一样的周期特性。（这里为什么用 $t_d=T/2$ 而不是其他值暂时还没有想法，目前的想法是，间隔半个周期一个对标的是线D的形式，一个在上升沿则另一个会在下降沿，这么间隔 $t_d=T/2$ 求差之后就能比较好地反应出信号的跳变信息，但实际上仿真的时候可以看出，在 $t_d=T/4$ 到 $t_d=3T/4$ 之间似乎没有很大的区别）。

从线G来看，能发现只有在初始信号有跳变的时候波形才会摆动，不然波形会归0。对线G进行平方，可以得到线H，可以看出，这样也生成了一个原型时钟，而定时误差信息可以通过计算 $E(r)$ 和 $L(r)$ 的差值获得。

$$ u_{t}(r)=E(r)-L(r-1) $$

其中，$E(r)$ 是第 $r$ 个符号的采样点，而 $L(r-1)$ 是第 $r-1$ 个符号的采样点，$E$ 对应的是提前的采样点， $L$ 对应的是滞后的采样点。

接下来就是化简这个函数了。首先有

$$ x_{d}(t)=x(t)-x(t-T / 2) $$

平方后为

$$ x_{d}^{2}(t)=x^{2}(t)+x^{2}(t-T / 2)-2 x(t) x(t-T / 2) $$

在 $t=r T+\tau$ 和 $r T+\tau-T / 2$ 处采样，有

$$ \begin{aligned} E(r)=& x_{d}^{2}(r T+\tau) \\ =& x^{2}(\tau+r T)+x^{2}(\tau+(r-1 / 2) T) \\ &-2 x(\tau+r T) x(\tau+(r-1 / 2) T) \end{aligned} $$

和

$$ \begin{aligned} &L(r-1)=x^{2}(\tau+(r-1 / 2) T)+x^{2}(\tau+(r-1) T) \\ &-2 x(\tau+(r-1 / 2) T) x(\tau+(r-1) T) \end{aligned} $$

令

$$ u_{t}(r)=L(r-1)-E(r) $$

将上式化简后可得

$$ \begin{aligned} &u_{t}(r)=x^{2}(\tau+(r-1) T)-x^{2}(\tau+r T) \\ &+2 x(\tau+(r-1 / 2) T){x(\tau+r T)-x(\tau+(r-1) T)} \end{aligned} $$

上式能不能作为定时误差项呢？其实可以了，因为包含了定时误差信息在里面了，不过还可以继续化简。对上式求均值，有

$$ \begin{aligned} &U_{t}(\tau)=\operatorname{Avg}\lbrace x^{2}(\tau+(r-1) T)\rbrace-\operatorname{Avg}\lbrace x^{2}(\tau+r T)\rbrace \\ &+2 \operatorname{Avg}{x(\tau+(r-1 / 2) T)(x(\tau+r T)-x(\tau+(r-1) T))} \end{aligned} $$

上式中第一项和第二项是相同的，因为是同一个信号不同延时而已，是周期平稳的随机信号，这两项可以直接消掉。对于输出信号来说，这两项$x^2(\cdot)$ 来说，其存在并不会影响到有用信号的输出均值。剩下后面一项，这一项可以写为

$$ \begin{aligned} u_{t}(r) &=x(\tau+(r-1 / 2) T){x(\tau+r T)-x(\tau+(r-1) T)} \\ &=x(r-1 / 2){x(r)-x(r-1)} \end{aligned} $$

这就是化简之后的Gardner误差检测公式。

我们接下来写程序仿真看看

clc; clear; close all;

rand('seed', 1);
data = 2 * randi([0 1], 1, 20) - 1;
% data = 2 * [1 0 1 0 1 1 0 0 0 1 0 1 1 1 1 0] - 1;
span = 16;
sps = 100;
rrc = rcosdesign(1, span, sps);

data_shape = conv(upsample(data, sps), rrc, 'same');
data_match = conv(data_shape, rrc, 'same');
data_Diff = data_match(floor(sps/2)+1:end) - data_match(1:end-floor(sps/2));
data_Diff2 = data_Diff .^ 2;

figure;
subplot(5, 1, 1);
plot(data_match);
title('data match');
grid on;
subplot(5, 1, 2);
plot(data_match(floor(sps/2)+1:end));
title('data match 1');
grid on;
subplot(5, 1, 3);
plot(data_match(1:end-floor(sps/2)));
title('data match 2');
grid on;
subplot(5, 1, 4);
plot(data_Diff);
title('data diff');
grid on;
subplot(5, 1, 5);
plot(data_Diff2);
title('data diff2');
grid on;

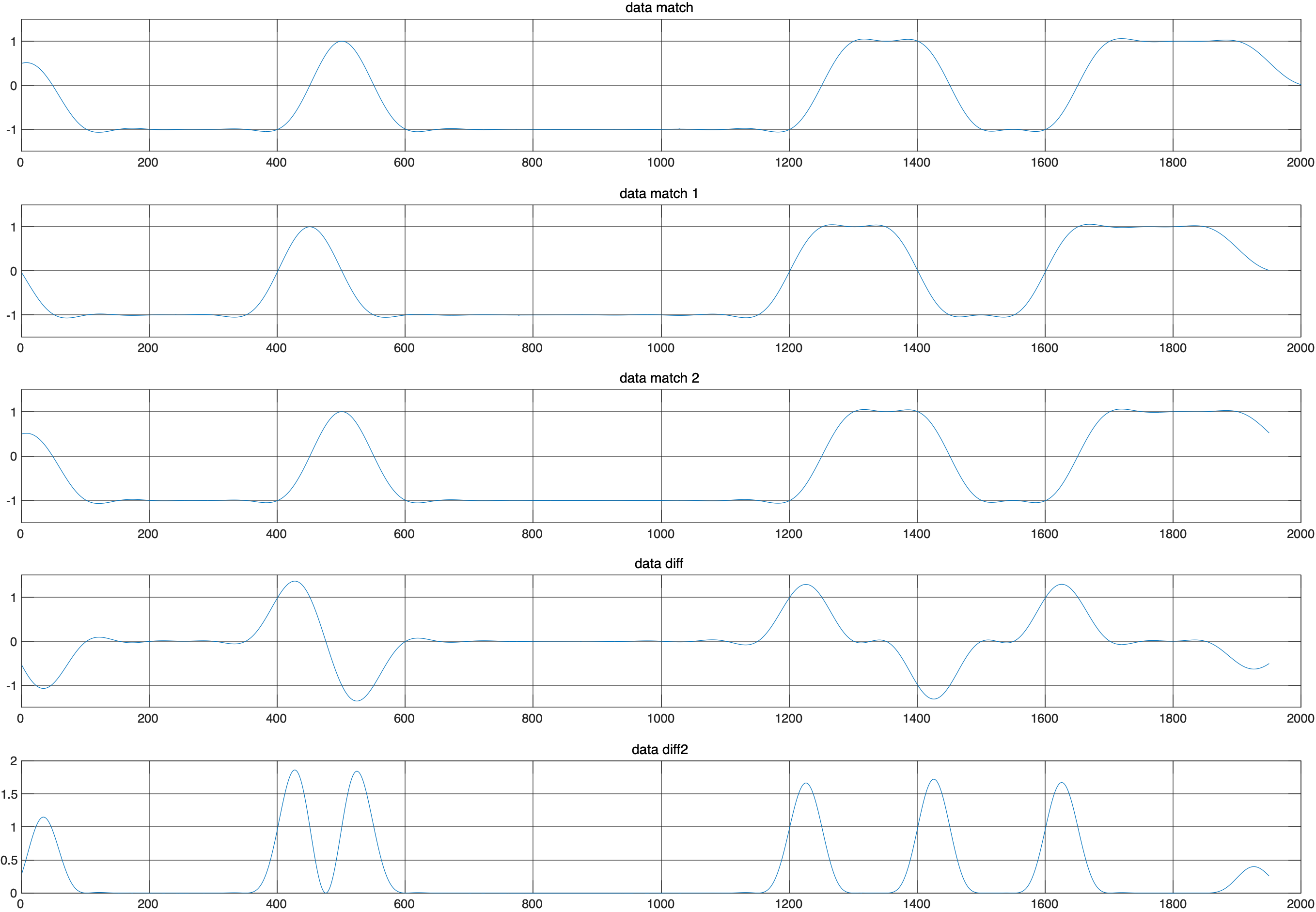
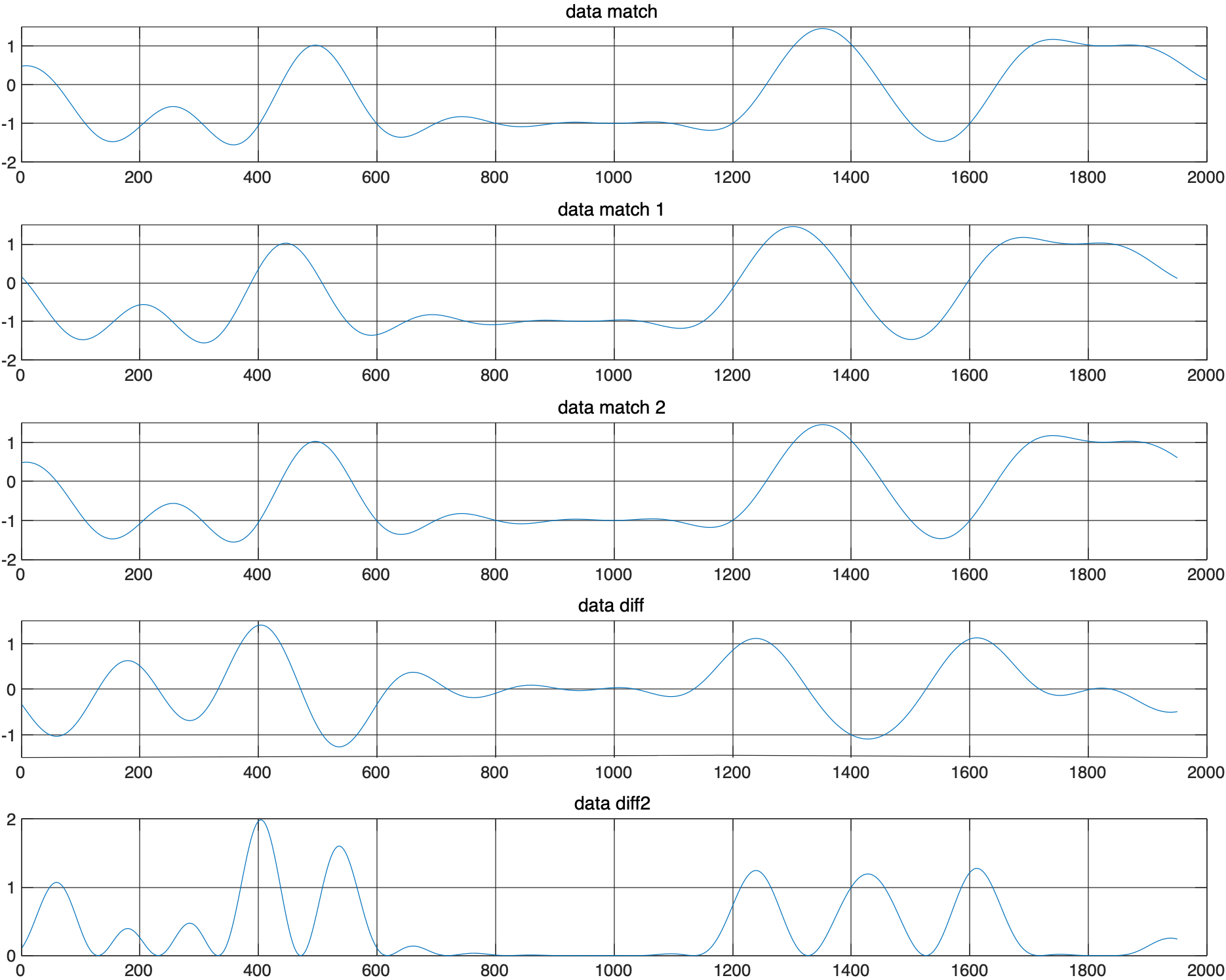
上图中最后两个图分别对应线G和线H，采用的成型系数为1，如果用 $L$ 和 $E$ 直接采然后作差，其实就相当于与对原始信号按照 $x(r-1 / 2){x(r)-x(r-1)}$ 求解。

程序都写了，不如我们改一下成型滤波器的$\alpha$，看看自噪声这个东西到底长啥样吧。 直接将成型系数改为0.1，则有下图

可以看出，成型系数变小之后，确实差了很多，引入了大量自噪声。

Gardner算法为何不受频偏影响？

首先假设一个时间连续且通过了滤波器后的复信号：

$$ w(t)={a(t)+j b(t)} e^{j \Delta \theta} $$

该复信号拆分成实部与虚部分别为：

$$ x_{R}(t)=a(t) \cos \Delta \theta-b(t) \sin \Delta \theta $$

$$ x_{I}(t)=a(t) \sin \Delta \theta+b(t) \cos \Delta \theta $$

其中$\Delta \theta$ 是载波相位误差，此处是随机的。对于定时误差估计，其算法为：

$$ \begin{aligned} u_{t}(t)&=x_{1}(t-T / 2)\left[x_{1}(t)-x_{1}(t-T)\right] \\ &+x_{2}(t-T / 2)\left[x_{2}(t)-x_{2}(t-T)\right] \end{aligned} $$

将其展开，有

$$ \begin{aligned} u_t(t)=&\left(a(t-\frac{T}{2})\cos(\Delta\theta)-b(t-\frac{T}{2})\sin(\Delta\theta)\right)\cdot \\ &\left[a(t)\cos(\Delta\theta)-b(t)\sin(\Delta\theta)-a(t-T)\cos(\Delta\theta)+b(t-T)\sin(\Delta\theta)\right] + \\ &\left(a(t-\frac{T}{2})\sin(\Delta\theta)+b(t-\frac{T}{2})\cos(\Delta\theta)\right)\cdot \\ &\left[a(t)\sin(\Delta\theta)+b(t)\cos(\Delta\theta)-a(t-T)\sin(\Delta\theta)-b(t-T)\cos(\Delta\theta)\right]\\ &=a(t-\frac{T}{2})\left[a(t)-a(t-T)\right] + b(t-\frac{T}{2})\left[b(t)-b(t-T)\right] \end{aligned} $$

从化简后的公式可以看出，载波频偏并不影响Gardner算法估计出来的定时误差。因此，Gardner算法可以用在载波恢复之前。