信道均衡算法

参考文献： 《高阶QAM信号盲均衡算法研究》 《Algorithms for Communications Systems and their Applications》 《Hybrid Methods for Blind Adaptive Equalization: New Results and Comparisons》

自适应均衡原理

自适应均衡器可以视为两部分组成：滤波子系统和自适应算法。所以本质上，均衡器也是一个滤波器，更严格地说，自适应均衡是自适应滤波器做补偿信道ISI来讲的一种应用。

自适应均衡问题建模

参考书籍：《Algorithms for Communications Systems and their Applications》 From the knowledge of the probability distribution of the channel input symbols $\lbrace a_k\rbrace$ and from the observation of the channel output sequence $\lbrace x_k\rbrace$, we want to find an equalizer $C$ such that the overall system impulse response is inter-symbol interference (ISI) free.

假设一个非最小相位系统的有理传递函数为

$$ H(z)=H_{0} \frac{P_{1}(z) P_{2}(z)}{P_{3}(z)} $$

其中， $H_ 0$为增益， $P_ 3(z)$ 和 $P_ 1(z)$ 为在单位圆内有零点的一次多项式，而 $P_ 2(z)$ 为在单位圆外有零点的一次多项式。对 $P_ 1(z)$ 和 $P_ 2(z)$ 求逆并用劳伦变换表示，为

$$ \begin{aligned} &P_{1}^{-1}(z)=\sum_{n=0}^{+\infty} c_{1, n} z^{-n} \ &P_{2}^{-1}(z)=\sum_{n=-\infty}^{0} c_{2, n} z^{-n} \end{aligned} $$

因此有

$$ H^{-1}(z)=\frac{1}{H_{0}} P_{3}(z)\left(\sum_{n=0}^{+\infty} c_{1, n} z^{-n}\right)\left(\sum_{n=-\infty}^{0} c_{2, n} z^{-n}\right) $$

由于输入信号是对称的，即 $\left\lbrace-a_{k}\right\rbrace$ 和 $\left\lbrace-a_{k}\right\rbrace$ 有相同的统计特性，因此，我们无法区分目标均衡器为 $H^{-1}$ 还是 $-H^{-1}$。所以均衡器的解为 $C=\pm H^{-1}$ ，这能令整个系统的响应为 $\Psi=\pm I$。

定理

如果输入符号是非高斯的，若输出符号

$$ y_{k}=\sum_{n=-\infty}^{+\infty} c_{n} x_{k-n} $$

的输入输出服从同分布，则系统$\Psi=\pm I$。

利用上述定理可以确定均衡器 $C$ 是否令输出分布收敛于输入分布。令代价函数为

$$ J=E\left[\Phi\left(y_{k}\right)\right] $$

其中 $\Phi$ 是选定的实数偶函数，则最优解为

$$ C_{o p t}(z)=\arg \min _{C(z)} J $$

这样就能找到$\pm H^{-1}$时的$c$值。

假设均衡器系数长为$N$，则

$$ \boldsymbol{c}_ {k}=\left[c_ {0, k}, c_{1, k}, \ldots, c_{N-1, k}\right]^{T} $$

令输入为

$$ \boldsymbol{x}_ {k}=\left[x_ {k}, x_{k-1}, \ldots, x_{k-(N-1)}\right]^{T} $$

有输出

$$ y_{k}=\sum_{n=0}^{N-1} c_{n, k} x_{k-n}=c_{k}^{T} \boldsymbol{x}_ {k} $$

同理，可以将系数简化为

$$ c_{o p t}=\arg \min_{c} J $$

假设$\Phi$的导数为$\Theta$，$J$关于$c$的梯度为

$$ \nabla_{c} J=E\left[\boldsymbol{x}_{k}\Theta (y_k)\right] $$

为了最小化$J$，使用随机梯度下降算法

$$ c_{k+1}=c_{k}-\mu \Theta\left(y_{k}\right) \boldsymbol{x}_{k} $$

其中 $\mu$ 是自适应增益。值得注意的是，收敛到 $H^{-1}$ 还是 $-H^{-1}$ 取决于初始系数$C$的选择。

均衡器迭代时所选择的代价函数 $\Phi$ 很重要。

PAM系统中的Sato算法

Sato代价函数定义为：

$$ J=E\left[\frac{1}{2} y_{k}^{2}-\gamma_{S}\left|y_{k}\right|\right] $$

其中

$$ \gamma_{S}=\frac{E\left[a_{k}^{2}\right]}{E\left[\left|a_{k}\right|\right]} $$

$J$ 的梯度为

$$ \nabla_{\boldsymbol{c}} J=E\left[\boldsymbol{x}_ {k}\left(y_{k}-\gamma_{S} \operatorname{sgn}\left(y_{k}\right)\right)\right] $$

引入信号

$$ \epsilon_{S, k}=y_{k}-\gamma_{S} \operatorname{sgn}\left(y_{k}\right) $$

假设自训练时伪误差的期望替代最小均方(LMS)判决算法中的误差项。其中，LMS算法的误差信号为

$$ e_{k}=y_{k}-\hat{a}_ {k} $$

其中，$ \hat{a}_ {k}$为符号 $a_ k$的判决，这是对样本 $y_ k$ 通过阈值判决器判决出来的结果。下图展示了输出样本$y_ k$时伪误差$\epsilon_{S, k}$的函数。

因此，Sato算法系数更新过程为

$$ \boldsymbol{c}_ {k+1}=\boldsymbol{c}_ {k}-\mu \epsilon_ {S, k} \boldsymbol{x}_ {k} $$

通过证明可知，如果输出符号$\lbrace a_{k}\rbrace$是sub-Gaussian的，那么Sato代价函数在一定的滞后后能将系统导向唯一的$C=\pm H^{-1}$。

Sato算法的局限性

1. 在得到Sato代价函数最小时的唯一点的前提是假设输入符号的概率分布是连续的，如果概率分布是离散的，Sato算法的收敛特性将会不理想；
2. 在$C=\pm H^{-1}$时，伪误差$\epsilon_{S, k}$并不为零，除非系统是二进制传输系统；
3. 伪误差的方差可以在期望解的邻域内为不可忽略的值。

值得一提的是，我们在最小化代价函数时，函数中有一项$E\left[\left|y_{k}\right|^{p}\right]$ ，其中$p\geq 2$ ，这意味着在代价函数中我们强调采样点幅值的贡献。

QAM系统中的自适应均衡

Constant-modulus algorithm（CMA，恒模算法）

最早由Godard提出，其代价函数为：

$$ J=E\left[\left(\left|\tilde{y}_ {k}\right|^{p}-R_{p}\right)^{2}\right]=E\left[\left(\left|y_{k}\right|^{p}-R_{p}\right)^{2}\right] $$

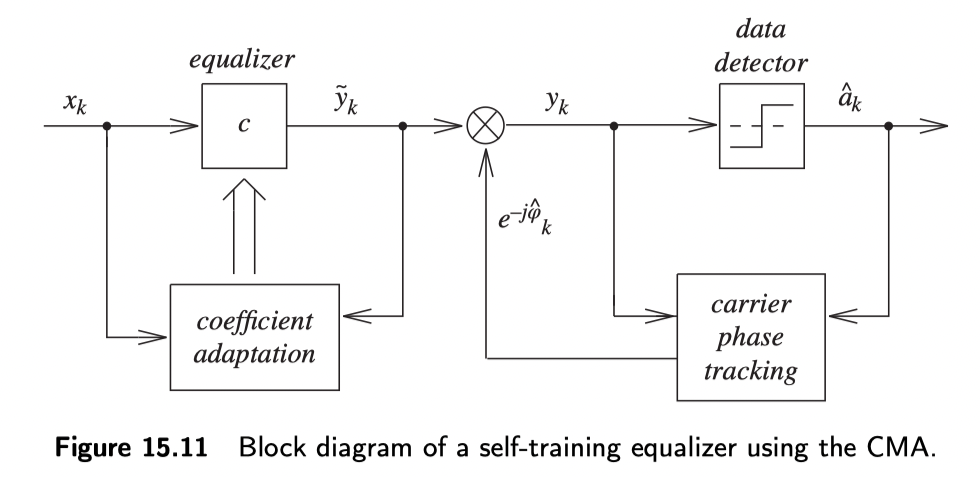
其中，$p$是一个参数，通常有 $p=1$ 或 $p=2$ 。由于代价函数 $J$ 取决于均衡器输出的绝对值的 $p$ 次方，因此，CMA不需要载波相位估计。下图是采用了CMA均衡器接收机的框图。

上式的梯度为

$$ \nabla_{c} J=2 p E\left[\left(\left|\tilde{y}_ {k}\right|^{p}-R_{p}\right)\left|\tilde{y}_ {k}\right|^{p-2} \tilde{y}_ {k} \boldsymbol{x}_ {k}^{*}\right] $$

常数$R_p$会选择成在均衡效果很好时令梯度为0的值，因此，有

$$ R_{p}=\frac{E\left[\left|a_{k}\right|^{2 p}\right]}{E\left[\left|a_{k}\right|^{p}\right]} $$

为啥这里需要用两个期望相除而不是相除后再求期望？ 因为相除后再求期望还有一项协方差需要求，而这两个随机变量都是$a_k$，协方差不为0，因此如果相除后再求期望的话就不是半径的$p$次方的期望了。

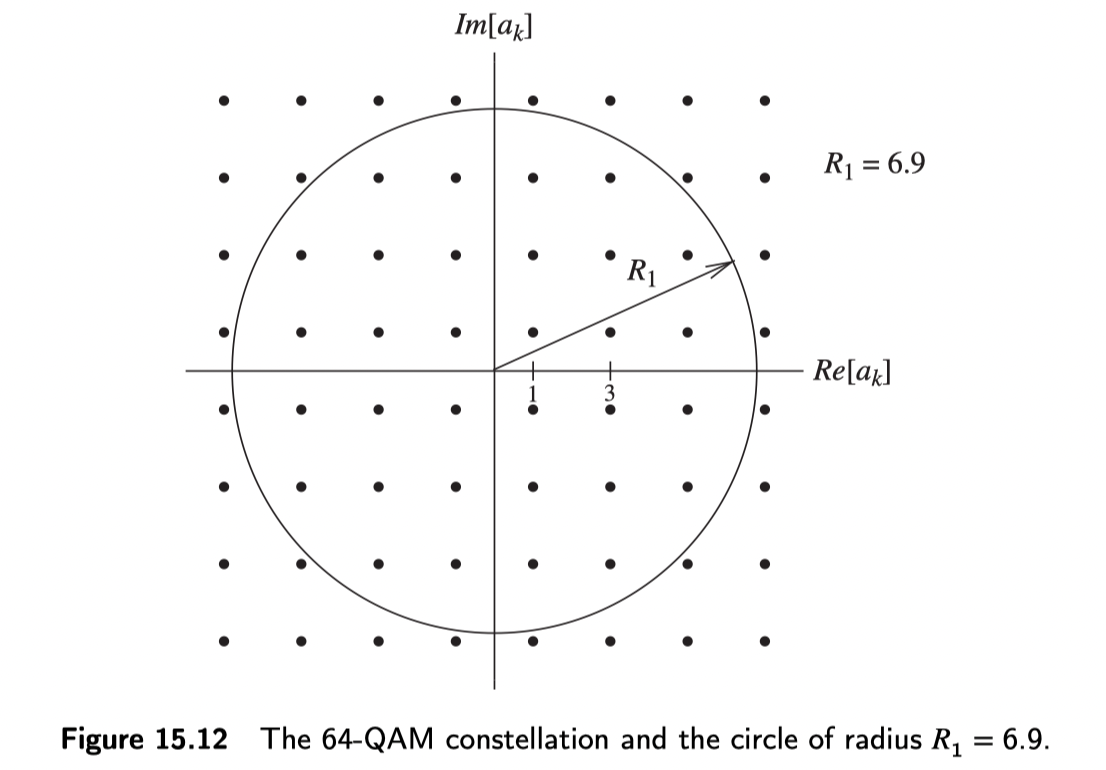
以64QAM星座图为例，利用上式，可以算出 $R_ 1 = 6.9$ 和 $R_ 2 = 58$。计算这两个半径的代码如下：

p = 2;
E1 = 0;
E2 = 0;
for i = 1:2:7
  for j = 1:2:7
    E1 = 1/16 * (sqrt(i^2+j^2) ^ p) + E1;
    E2 = 1/16 * (sqrt(i^2+j^2) ^ (2*p)) + E2;
  end
end
E2/E1

半径$R_ 1=6.9$的圆在64QAM星座图中的相对位置如下：

我们可以借助下式以利用梯度更新均衡器系数

$$ \boldsymbol{c}_ {k+1}=\boldsymbol{c}_ {k}-\mu\left(\left|\tilde{y}_ {k}\right|^{p}-R_{p}\right)\left|\tilde{y}_ {k}\right|^{p-2} \tilde{y}_ {k} \boldsymbol{x}_ {k}^{* } $$

对于 $p=1$ 的情况，上式化简成：

$$ \boldsymbol{c}_ {k+1}=\boldsymbol{c}_ {k}-\mu\left(\left|\tilde{y}_ {k}\right|-R_{1}\right) \frac{\tilde{y}_ {k}}{\left|\tilde{y}_ {k}\right|} \boldsymbol{x}_ {k}^{*} $$

这就是CMA算法，而Sato算法是CMA算法的一个特例。

CMA算法的优缺点

优点

1. 鲁棒性好
2. 复杂度低
3. 使用广泛
4. 可以在载波恢复之前

缺点

1. Time-to-convergence(TTC)较慢
2. 收敛时会有一个常数相位偏移

Multimodulus Algorithm(MMA)多模算法

参考文献：《Hybrid Methods for Blind Adaptive Equalization: New Results and Comparisons》

MMA将均衡器的输出分为同相分量与正交分量，对于方形的QAM星座图来说，MMA误差为

$$ \begin{array}{r} E_{n, R}^{m m a}=y_{n, R}\left(y_{n, R}^{2}-R_{M}\right) \ E_{n, I}^{m m a}=y_{n, I}\left(y_{n, I}^{2}-R_{M}\right) \ E_{n}^{m m a}=E_{n, R}^{m m a}+j \cdot E_{n, I}^{m m a} \end{array} $$

$R$ 和 $I$ 分别代表实数和虚数分量，$R_M$ 是一个常数，定义为：

$$ R_{M}=\frac{\mathrm{E}\left\lbrace a_{n}^{4}\right\rbrace}{\mathrm{E}\left\lbrace a_{n}^{2}\right\rbrace} $$

MMA算法优缺点

MMA算法对比CMA有更低的MSE，并且不需要相位恢复。然而，收敛速率与CMA是差不多的，并且鲁棒性更低。

Decision Directed(DD)算法

DD算法在更新均衡抽头的时候用符号估计替换掉符号统计值。DD误差定义如下：

$$ E_ {n}^{d d}=y_ {n}-\hat{s}_ {n} $$

其中 $\hat{s}_ {n}$ 是符号点的估计。

DD算法优缺点

DD算法有更低的MSE和更低的抖动。然而，只有当MSE低于一个固定的阈值的时候才会收敛，针对QAM星座图，有论文推导过其阈值。

Modified-CMA(MCMA)

相比CMA的误差函数，MCMA算法增加了一个星座图匹配误差项(constellation matched error, CME)。这能够极大地降低TTC和MSE。MCMA误差定义为：

$$ E_{n}^{m c m a}=y_{n}\left(\left|y_{n}\right|^{2}-R_{C}\right)+\beta \eta_{n} $$

其中$\beta$ 是CME权重因子，$\eta_ n$是CME项，其定义为：

$$ \eta_{n}=\left.\frac{d}{d x} g(x)\right|_ {x=y_ {n, R}}+\left.j \frac{d}{d x} g(x)\right|_ {x=y_ {n, I}} $$

其中$g(x)$是CME函数，该函数对QAM星座图来说在符号点上为0，$g(x)$定义为：

$$ g(x)=1-\sin ^{2 p}\left(\frac{x \pi}{2 d}\right) $$

其中，$p$是正整数，$d$ 是星座点间的距离。

MCMA算法优缺点

相比CMA算法有更低的MSE，更低的抖动以及更快的TTC。然而，该算法需要提前做相位恢复，并且复杂度更高，若CME项通过查找表实现的话，需要消耗大量面积。

CMA-MMA

CMA-MMA算法在代价函数中采用非对称的做法，在同相滤波器(in-phase filter)中使用CMA误差，在正交滤波器(quadrature filter)中使用MMA误差。CMA-MMA误差定义如下：

$$ \begin{array}{r} E_{n, R}^{c m a-m m a}=y_{n, R}\left(\left|y_{n}\right|^{2}-R_{C}\right) \ E_{n, I}^{c m a-m m a}=y_{n, I}\left(y_{n, I}^{2}-R_{M}\right) \ E_{n}^{c m a-m m a}=E_{n, R}^{c m a-m m a}+j \cdot E_{n, I}^{c m a-m m a} \end{array} $$

CMA-MMA算法优缺点

优点：

1. 相比CMA算法有更低的MSE
2. 鲁棒性好
3. 尽管MMA误差项会导致星座图旋转，也不需要提前做相位恢复

缺点：

1. 收敛速率差不多
2. 可能会导致较大的抖动

CMA-Assisted Decision Adjusted Modulus Algorithm(CADAMA)

CADAMA是一种双模式算法，首先用CMA来减小MSE来让改进第二模式中的判决步骤。The decision adjusted modulus algorithm(DAMA)的代价函数对每个QAM中的环来说都是0，将DAMA用在第二模式中，DAMA误差项定义为：

$$ E_{n}^{d a m a}=\min _ {i}\left[y_ {n}\left(\left|y_{n}\right|^{2}-R_{i}\right)\right] $$

其中，$1 \leq i \leq p$ 且 $\left\lbrace R_{i}\right\rbrace_{i=1}^{p}$ 是QAM星座图中信号点对应的半径，$p$是大于1的整数。

CADAMA算法的优缺点

优点：

1. 有更低的MSE
2. 比CMA有更低的抖动

缺点：

1. 对于高阶QAM星座图来说需要更多的判决区域，这增加了选区错误的可能性
2. 在信道失真严重时，DAMA算法代价函数的错误率太大，DAMA算法不能收敛，因此在均衡的初始阶段，使用DAMA算法不可靠，不能冷启动DAMA算法

CMA算法与DAMA算法之间的转换准则

CADAMA需要首先采用CMA来实现均衡器的初始化调整，并且当幅度均衡完成之后，切换到DAMA模式。由于DAMA是使每个QAM星座图中的圈对应的代价函数归为0来实现的，因此对于很多标准QAM星座图来说，其抖动可以降低18到25dB。

CMA与DAMA的切换准则：使用goodness-of-fit test来对观测间隔内的半径直方图与QAM星座图的半径分布模板进行比较来指导切换的。

QAM星座图半径分布模板

令 $p_ i$ 代表信号点半径 $i$ 的模板概率，则有 $p_i = (\text{number of signal points on radius} \quad i)/M$，其中 $M$ 为调制阶数，且有$\sum_{i=1}^{\rho} p_{i}=1$。

观测间隔

用 $N$ 来表示观测间隔，其与 $M$ 的关系为：$N=\kappa M$，观测间隔 $\kappa M$ 可以生成一个针对每个符号 $a_ m$ 的观测值 $K$。此处可以采用 $\kappa = 20$。

盲均衡性能评价准则

收敛速度

一个具有较高收敛能力的算法通常冷启动能力比较强，即算法是“易于收敛”的。

均方判决误差

均方误差MSE的定义：

$$ M S E=E\left\lbrace|d(n)-\mathrm{y}(n)|^{2}\right\rbrace $$

其中，$d(n)$是期望信号，$y(n)$是均衡器输出。

剩余ISI

定义盲均衡算法的评价指数ISI，表达式为：

$$ \operatorname{ISI}(n)=\frac{\sum\left|\mathbf{h}_ {w}(n)\right|^{2}-\max \left|\mathbf{h}_ {w}(n)\right|^{2}}{\max \left|\mathbf{h}_{w}(n)\right|^{2}} $$

$\operatorname{ISI}(n)$ 表示第 $n$ 次迭代后的剩余码间干扰， $\sum\left|\mathbf{h}_ {w}(n)\right|^{2}$ 表示对联合冲激响应 $\mathbf{h}_ {w}(n)$ 的所有 $n$ 求平方之和， $\max \left|\mathbf{h}_ {w}(n)\right|^{2}$ 表示联合冲激相应 $\mathbf{h}_{w}(n)$ 最大的一项的平方。

误符号率

多数情况下，误符号率和盲均衡算法的均方判决误差以及剩余ISI是一致的。