BI-AWGN信道接收概率初始化

内容参考：《Iterative Error Correction Turbo, Low-Density》

接收信号概率一般怎么衡量？

用Log likelihood ratios (LLRs)对数似然比来衡量。LLR定义如下：

$$ L(x)=\log \frac{p(x=0)}{p(x=1)} $$

其中$p(x=1)=1-p(x=0)$，log是以自然对数$e$为底的。若$p(x=0)>p(x=1)$，有$L(x)$为正。

若给定LLRs，可以利用下述公式反求概率值：

$$ p(x=1)=\frac{p(x=1) / p(x=0)}{1+p(x=1) / p(x=0)}=\frac{e^{-L(x)}}{1+e^{-L(x)}} $$

$$ p(x=0)=\frac{p(x=0) / p(x=1)}{1+p(x=0) / p(x=1)}=\frac{e^{L(x)}}{1+e^{L(x)}} $$

用对数来表达概率值的一个好处是当概率之间需要用乘法的时候，换成对数就可以只用加法进行了，可以节省实现复杂度。

BI-AWGN信道接收概率初始化

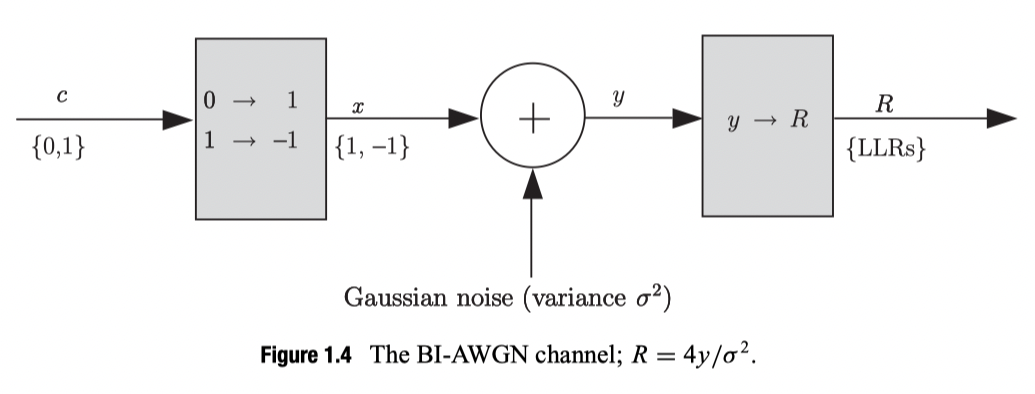
Binary-input additive white Gaussian noise (BI-AWGN)信道可以用方程描述如下：

$$ y_{i}=\mu x_{i}+z_{i} $$

其中，$x_i\in {-1, +1}$是第$i$个传输符号，$y_i$是第$i$个接收符号，$z_i$是服从均值为0，方差为$\delta^2$高斯随机分布的加性噪声。很多时候会写成$z_i=AWGN(0, \delta)$的形式。

$z$的概率密度函数为

$$ p(z)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-z^{2} / 2 \sigma^{2}} $$

当在BI-AWGN信道传输二进制码字时，码字比特$c_i\in {0, 1}$可以按以下两种方式映射为符号$x_i\in {-1, +1}$： ${0 \rightarrow 1,1 \rightarrow-1}$ 或 ${0 \rightarrow-1,1 \rightarrow 1}$。此处以${0 \rightarrow 1,1 \rightarrow-1}$举例。

BI-AWGN信道接收到的LLRs为

$$ \begin{aligned} R_{i}=L\left(x_{i} \mid y_{i}\right) &=\log \frac{p\left(c_{i}=0 \mid y_{i}\right)}{p\left(c_{i}=1 \mid y_{i}\right)} \\ &=\log \frac{p\left(x_{i}=1 \mid y_{i}\right)}{p\left(x_{i}=-1 \mid y_{i}\right)} \\ &=\log \frac{p\left(y_{i} \mid x_{i}=1\right) p\left(x_{i}=1\right) / p\left(y_{i}\right)}{p\left(y_{i} \mid x_{i}=-1\right) p\left(x_{i}=-1\right) / p\left(y_{i}\right)} \\ &=\log \frac{p\left(y_{i} \mid x_{i}=1\right) p\left(x_{i}=1\right)}{p\left(y_{i} \mid x_{i}=-1\right) p\left(x_{i}=-1\right)} \end{aligned} $$

其中用到了贝叶斯公式：$p\left(x_{i} \mid y_{i}\right)=p\left(x_{i}, y_{i}\right) / p\left(y_{i}\right)=p\left(y_{i} \mid x_{i}\right) p\left(x_{i}\right) / p\left(y_{i}\right)$，如果符号等概出现，即$p(x_i=-1)=p(x_i=1)$，则有

$$ R_{i}=L\left(x_{i} \mid y_{i}\right)=\log \frac{p\left(y_{i} \mid x_{i}=1\right)}{p\left(y_{i} \mid x_{i}=-1\right)} $$

对于BI_AWGN信道来说，有

$$ \begin{aligned} p\left(y_{i} \mid x_{i}=1\right) &=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\left(y_{i}-\mu\right)^{2}}{2 \sigma^{2}}\right) \\ p\left(y_{i} \mid x_{i}=-1\right) &=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\left(y_{i}+\mu\right)^{2}}{2 \sigma^{2}}\right) \end{aligned} $$

则对LLRs化简，有

$$ \begin{aligned} R_{i}=L\left(x_{i} \mid y_{i}\right) &=\log \frac{\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\left(y_{i}-\mu\right)^{2}}{2 \sigma^{2}}\right)}{\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\left(y_{i}+\mu\right)^{2}}{2 \sigma^{2}}\right)} \\ &=\log \exp \left(-\frac{\left(y_{i}-\mu\right)^{2}}{2 \sigma^{2}}+\frac{\left(y_{i}+\mu\right)^{2}}{2 \sigma^{2}}\right) \\ &=\frac{1}{2 \sigma^{2}}\left(-\left(y_{i}^{2}-2 \mu y_{i}+\mu^{2}\right)+\left(y_{i}^{2}+2 \mu y_{i}+\mu^{2}\right)\right) \\ &=\frac{2 \mu}{\sigma^{2}} y_{i} \end{aligned} $$

对于比特$c_i$的LLR值，有时被称作$c_i$的软判决。$c_i$的硬判决指的是，当$R_i$为正值时，返回 $c_i=0$ 或 $x_i=1$，若$R_i$为负值时，返回 $c_i=1$ 或 $x_i=-1$。

其他变形

若考虑BI-AWGN信道噪声水平的相对值，将$\mu=1$并通过调节$\delta$来反映信道的噪声水平会方便一些，此时$R_i$可以写为：

$$ R_{i}=\frac{2}{\sigma^{2}} y_{i} $$

表示为$E_b/N_0$的形式

噪声水平通常会通过每符号能量$E_s$与噪声谱密度$N_0$之比来表示：

$$ \frac{E_{s}}{N_{0}}=\frac{\mu^{2}}{2 \sigma^{2}} $$

之因此式$y_{i}=\mu x_{i}+z_{i}$有时会写成如下形式：

$$ y_{i}=\sqrt{E_{s}} x_{i}+z_{i} $$

对于BI-AWGN信道，以$r$作为信息比特与传输比特之比，即码率，对于二进制输入，$E_s$代表的就是每传输比特的能量。

对于使用了纠错编码的信道来说，噪声水平经常用$E_b/N_0$来表示，其中$E_b$是每信息比特的能量。

有

$$ \frac{E_{b}}{N_{0}}=\frac{1}{r} \frac{E_{s}}{N_{0}}=\frac{1}{r} \frac{\mu^{2}}{2 \sigma^{2}} $$

则接收的LLR表示为：

$$ R_{i}=L\left(x_{i} \mid y_{i}\right)=4 \frac{\sqrt{E_{s}}}{N_{0}} y_{i}=4 \frac{\sqrt{r E_{b}}}{N_{0}} y_{i} $$

当$\mu$为1时，有

$$ R_{i}=\frac{4}{N_{0}} y_{i} $$

其中，$E_b/N_0$还可以表示为dB的形式：

$$ \frac{E_{b}}{N_{0}}(\mathrm{~dB})=10 \log _ {10} \frac{E_ {b}}{N_{0}}=10 \log _{10} \frac{\mu^{2}}{2 r \sigma^{2}} $$

值得注意的是，$E_s$代表的是每传输符号（二进制输入则对应为比特）的能量，是传输符号而不是信息符号，而$E_b$代表的是每信息比特的能量，这两者隔了个码率。